Learn
Proof of agreement
If you've spent long enough on the Stellar network, perhaps one of the mysteries you ponder is how Stellar’s unique Proof-of-Agreement (PoA) consensus algorithm works. After all, this is not Proof-of-Stake or Proof-of-Work – so what could it be?

The mechanism
The Proof-of-Agreement mechanism is a very interesting and individual take on the problem of attaining consensus in a permissionless distributed system (“permissionless” meaning that no central authority controls who joins the network). Read on, and all will be revealed … using examples of how Proof-of-Agreement can work in real life!
Example 1
Amy's anniversary gift
Bob must choose an anniversary gift for his wife Amy: flowers or chocolate?
Bob trusts his friends Cal and Cam, and his mother-in-law Deb. We can say that he has two quorums for making a decision about matters concerning Amy:
- Bob, Cal, and Cam, and
- Bob and Deb.
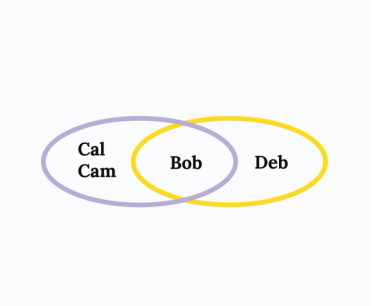

For Bob to decide on an anniversary gift, agreement within at least one of these quorums is required. That is:
- Either Bob, Cal, and Cam agree,
- Or Bob and Deb agree.
It might also be that Bob, Cal, Cam, and Deb all agree, but this is not needed for deciding on a gift.
Note that making progress is compulsory; it’s not an option for Bob to give up and explain to Amy that he didn’t get her an anniversary gift because he couldn’t decide on what to get.
So to make progress towards buying a suitable gift, Bob needs to establish the opinions of Cal and Cam, and/or of Deb.
Let’s think like programmers and list all possible cases:
- Cal and Cam recommend flowers. Deb recommends flowers too.
Bob has to agree with at least one of his quorums, and since both quorums are saying the same thing, Bob has no choice: in order to progress, he must agree with them and buy flowers.1 - Cal and Cam recommend chocolate. Deb recommends flowers.
Here, Bob has a choice: he can progress with either flowers or chocolate. In either case, one of his quorums will be in agreement.
Bob makes his choice by tossing a coin, or he might use background knowledge. - Cal recommends chocolate, Cam recommends flowers. Deb recommends flowers.
Unless Bob can convince Cal or Cam to change their mind, Bob has to go with flowers.
This is because the quorum Cal, Cam, Bob cannot be in agreement no matter what Bob does (because Cal and Cam disagree), but Bob can form a quorum with Deb by buying flowers. - Cal recommends chocolate, Cam recommends flowers. Deb recommends chocolate.
As for case 3, Bob has no choice: he has to agree with Deb and buy chocolate.
Let's Think Like Programmers
Possible cases
Cal and Cam recommend flowers. Deb recommends flowers too.
Bob has to agree with at least one of his quorums, and since both quorums are saying the same thing, Bob has no choice: in order to progress, he must agree with them and buy flowers.1
Cal and Cam recommend chocolate. Deb recommends flowers.
Here, Bob has a choice: he can progress with either flowers or chocolate. In either case, one of his quorums will be in agreement.
Bob makes his choice by tossing a coin, or he might use background knowledge.
Cal recommends chocolate, Cam recommends flowers. Deb recommends flowers.
Unless Bob can convince Cal or Cam to change their mind, Bob has to go with flowers.
This is because the quorum Cal, Cam, Bob cannot be in agreement no matter what Bob does (because Cal and Cam disagree), but Bob can form a quorum with Deb by buying flowers.
Cal recommends chocolate, Cam recommends flowers. Deb recommends chocolate.
As for case 3, Bob has no choice: he has to agree with Deb and buy chocolate.
Comments
Amy's anniversary gift
The anniversary example captures some useful aspects of how Stellar works:
- The basic action is ownership transfer: of tokens in the case of Stellar; of flowers or chocolate in the case of Bob above.
- Making progress is compulsory: Bob has to give Alice a present (assuming he wants to stay married), and Stellar has to make progress (assuming it wants to retain users).
There are also differences. The anniversary example has a fixed number of (four) participants, two fixed quorums, and just one decision. Stellar has dozens of validator nodes, makes decisions every two to five seconds – and, at least in principle, new validator nodes can join any time.
How is this process managed?
Example 2
Amy and bob's wedding list
When a new validator node joins the Stellar network, it nominates a set of slices (also called a witness). A quorum is then any set of validators such that for each validator in that set, one of its slices is also in that set.
To illustrate how this works, let’s go back to when Amy and Bob were planning their wedding. They were drafting their wedding invite list …
- Amy wanted to invite Bob (of course), her best friend Che, and her father Dee.
So Amy has one slice, which we write in maths sets notation as follows:
{Bob, Che, Dee}. - Bob wanted to invite Amy (of course), his parents Hal and Ivy, and at least one of his friends Gia or Guy.
So Bob has two slices:
{Amy, Hal, Ivy, Gia}
and {Amy, Hal, Ivy, Guy}. - Che is fine coming on his own.
So Che has one empty slice:
{}
(or one slice, which is {Che}; it amounts to the same thing). - Dee will only come if his wife Deb can come too, and vice versa. They each have one slice, which is each other.
- Ivy will only come if her sister Kay comes too.
- Guy wants to bring either Jan or Joe. So Guy has two slices:
{Jan}, and {Joe}. - Jan and Joe are fine coming on their own.


The invite list has to be a quorum: every invitee must have at least one of their slices at the wedding.
So for example: Amy must bring Che and Dee, but Bob can bring (at least) one of: Hal, Ivy, and Gia; or Hal, Ivy, and Guy. Running the calculations we see that possible invite lists/quorums (starting from Amy and Bob) are:
- {Amy, Che, Dee, Hal, Ivy, Gia, Deb, Kay}
- {Amy, Che, Dee, Hal, Ivy, Guy, Deb, Kay, Jan}
- {Amy, Che, Dee, Hal, Ivy, Guy, Deb, Kay, Joe}
To get a feeling for how this works, note that:
- Once we add Amy, we have to add Bob (already there), Che, and Dee.
- Once we add Bob, we have to add Amy (already there) and Hal and Ivy – because they are in all of Bob’s slices – but we can choose whether to add Gia or Guy.
- Once we add Guy, we have to add at least one of Jan and Joe.
- Once we add Dee, we have to add Deb, and vice versa (but Dee is already there).
Continuing in this way, we grow the invite list until we reach what mathematicians call a fixed point. This is our quorum.
The invite lists above are the smallest possible quorums. Larger quorums may make for a nicer wedding party, but also for a more expensive one. Often, couples solve the wedding party quorum problem by inviting everybody, which is a mathematically valid solution, though it is resource-intensive (to borrow another programming term).
We leave it as an exercise to the reader to create a set of slices for the anniversary example above. (The answer is in a footnote!2)
Stellar builds quorums up from slices, just like Amy and Bob did when they built their invite list.
- Start from some participant or participants (e.g. Amy and Bob); then
- for each member of the set, add one of its slices; and
- repeat until every participant is accompanied by (at least) one of its slices.
In Stellar, slices represent trust. When you join the network as a validator, you have to say what slices of existing validators you trust. A quorum is a set that can make progress, in the sense that if it is in agreement, then everybody in the quorum is in agreement with at least one trusted group.

Example 2
Romas residences' AGM
Let’s recap the story so far:
- When a validator joins the Stellar network, it nominates some trusted slices.
- A quorum is a set of validators that has at least one slice of each validator in the quorum.
- When a quorum is in agreement, it can progress (e.g. by committing a transaction to the ledger).
What stops such a system from dissolving into chaos, with different validators in different quorums committing different transactions? For this, we need a technical definition.
Definitions
Intertwined & topen
- Call two participants p and q intertwined when every quorum P of p intersects with every quorum Q of q.
- A topen is a quorum of intertwined participants.
In Example 1 above, all participants Cal, Cam, Bob, and Deb are intertwined, and the system consists of a single topen.
Let’s go back to Amy and Bob. They live in a block of flats called Roma Residences. Roma Residences is one of three blocks in the neighbourhood, the other two being London Residences and Paris Residences.
At Roma’s AGM (annual general meeting), decisions are made by majority vote. So quorums are majorities of participants, and all Roma residents are intertwined because all majority sets intersect (otherwise it would not be a majority). Similarly for London and Paris. However, the Roma quorums do not intersect with the London or Paris quorums, nor vice-versa.
So this system partitions into three disjoint topens, each capable of making progress independently: the AGM councils of Roma, London, and Paris Residences respectively. This is very intuitive: we expect these committees to act autonomously and coherently within themselves, and in mathematical terminology we just say that these are three disjoint topen sets.

Let’s look at two more concrete examples, to get a feel for how being intertwined works:
The upper example has four quorums (labelled A, B, C, and D) and all participants are intertwined.
In the lower example the reader can check that 3 and 4 are intertwined just with themselves, and -1, 1, 2, and 0 are intertwined with one another. There are three topen sets: 3; 4; and -1, 1, 2 (but not -1, 1, 2, 0).3
The Roma/London/Paris example is canonical, because it can be proved (using mathematics that is not in this blog post) that:
Definitions
Lemma
Any quorum system will partition itself into disjoint topens (plus perhaps some isolated points).
Consensus is guaranteed within each topen, by the intertwined property: if every participant agrees with its quorum, and all quorums in the topen intersect, then every participant in the topen must agree.
Example 4
Influence requires reciprocated trust
Blockchain systems are supposed to be resilient under attack. Let’s consider how this works in Stellar.
Suppose the Paris residents want to corrupt decision-making in Roma Residences. The Paris residents can add the Roma residents to their own slices (and so create new quorums) – but they cannot change the Roma residents’ slices (each participant decides their own slices and only their own slices). This means that the Roma residents’ topen – their AGM council – is unaffected by the attack, and Roma can continue to make decisions and progress, completely unaffected by the fact that they are in the slices of external parties whose trust they do not reciprocate.
This simple example matters particularly because it is so different from how blockchains like Ethereum work, where anybody on the network with computation or stake gets a seat on the voting table, no matter how unsavoury they may be as a person or organisation. In Stellar, you only get a seat on a table if you can convince those already at that table to trust you. Or to put this in more technical language – the only way to attack decision-making of a topen is to convince members of that topen to add the attacker to their slices. An untrusted attacker cannot affect their decision-making, no matter how powerful the attacker’s computers or how wealthy the attacker may be.
In Stellar, reputation – trustworthiness – is everything. In some respects this is a better system than PoW or PoS based systems (proof-of-work or proof-of-stake): trustworthiness is a social construct, not a computational one, so representing trust in the system gives participants incentives to curate and maintain their social reputation – in other words, to behave in an honest and reliable manner. Reputation may be an imperfect predictor of virtue, but at least, while anyone with resources can obtain mining hardware or stake, not anyone can win trust and respect.
Final Words
It's a bit more complex
In real life, making Stellar work is a bit more complex than the examples above. We can’t go into the details here but we’d like to give the reader a flavour of the issues involved in applying these ideas in practice.
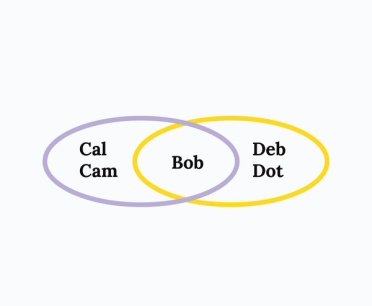
The relevant example is quite simple. Consider an elaboration of Example 1 above in which all quorums have size at least three:
All we have done is to add Bob’s mother, Dot, to the quorum that contained Bob’s mother-in-law Deb.
This is a simple change – but it means that if Cal and Cam disagree, and also Deb and Dot disagree, then quorum agreement is impossible regardless of Bob’s vote (any resemblance to real life here is purely coincidental, of course).
In real life what happens is that quorums debate amongst themselves until such time as one of the quorums (hopefully) reaches agreement and can progress. (In real life this always happens reasonably, in good faith, and without feuding or rancour, of course.) Something similar is formalised within the Stellar Consensus Protocol, by a computational mechanism which reliably attains consensus, within seconds. We look forward to diving into this amazing technical accomplishment in another blog post.
1. You might be wondering what happens if Bob goes and buys chocolates anyway. Well he could, but that just wouldn’t be playing by the rules. Life is full of such situations, and English has positive words for those that play by the rules (reputable, reliable, trustworthy) and negative words for those who don’t (disreputable, unreliable, untrustworthy).
2. One possibility is:
Bob has two slices:
- {Cal, Cam} and {Deb}.
- Deb has one slice, {Bob}.
- Cal has one slice, {Bob}.
- Cam has one slice, {Bob}.
Other slices can generate the same quorums.
3-1, 1, 2, and 0 is not a topen: all the elements are intertwined, and it contains a quorum, but it is not in itself a quorum.
Next Steps