Behind the Scenes with SPEEDEX

Integrating SPEEDEX with Stellar would require three main changes.

1. A multi-phase ledger application process

Stellar would create a new "Commutative" transaction type. Mathematically, two operations "commute" if they can be applied in any order without changing the end result. These transactions will be run as the first phase of applying a ledger. These "commutative" transactions would only be allowed to contain "commutative" operation codes.

Initially, the only "commutative" operation code would be a new "Create SPEEDEX Offer" operation code. SPEEDEX, by design, does not depend on the ordering of the offers in a batch. An operation, then, that just adds a new trade offer to an unordered set of offers naturally commutes with every other "Create SPEEDEX Offer" operation code.

These transactions would generate a batch of trades for SPEEDEX. SPEEDEX would then compute prices and transfer assets accordingly. Offers that do not immediately execute in one batch would not persist to the next batch.

Finally, Stellar-core would run the rest of the transactions in a ledger. These would have exactly the same semantics as existing Stellar transactions.

In the future, Stellar could add other operation codes to the commutative phase. Effectively parallelizing the internal operation of Stellar-core requires significant engineering work, so the initial implementation would run the commutative phase serially. The internal operation could then be parallelized without making any protocol changes. And in the long term, it is more effective and less work to accelerate a protocol that is designed to parallelize from the beginning, than to accelerate a protocol designed for serial execution (e.g. with speculative execution on a smart contract virtual machine). A general rule (the Scalable Commutativity Rule of Clements et. al.) is that a set of operations that commute can be parallelized effectively.

2. Extended Transaction Set Preconditions

SPEEDEX relies on a guarantee that every offer to sell an asset actually can provide that asset for sale. As the ordering between transactions should not matter, Stellar-core needs to verify that no two trade offers are selling the same underlying units of one asset (in other words, Stellar-core needs to prevent negative account balances, which would effectively result in double-spends).

Stellar-core can validate this requirement with a simple rule, ensuring that every account has enough assets to cover its selling obligations. For a given transaction set, Stellar-core will add up all the sell obligations of every account. The transaction set would be considered invalid if the sell obligations of any account exceed the account's balance (for any asset). This precondition essentially generalizes the Stellar protocol's existing XLM balance checks for paying transaction fees, and can be implemented in an analogous manner.

3. Issuance Limited Assets and Trustline Limits

The assets tradable on SPEEDEX would be restricted to having, in total, only INT64_MAX units issued across the Stellar ecosystem. Again, without a transaction ordering, the Stellar protocol does not have a method for resolving conflicts between transactions, and one conflict that could arise in SPEEDEX is one account receiving more than INT64_MAX units of one asset in total. Stellar can avoid this problem by limiting the total amount of any asset issued to at most INT64_MAX units.

This limit would not need to apply to every asset – only those traded through SPEEDEX. The protocol would also require users to set their trustline limits to INT64_MAX in order to transact through SPEEDEX.

The simplest version of SPEEDEX uses only limit orders. However, the algorithms for price computation, discussed below, and the overall SPEEDEX model also can naturally mix AMMs and limit orders with minimal modifications. And more importantly, SPEEDEX could leverage Stellar's recently launched AMM functionality without any modifications to the AMMs or to the regular "noncommutative" transactions.

An AMM can answer the question "to move the AMM's marginal exchange rate from its current state to the auctioneers exchange rate, how much of one asset would the AMM have to sell to the auctioneer?" The AMM would then receive in exchange the corresponding amount of the AMM's other asset, exchanged at the auctioneer's rate.

From Arrow-Debreu Exchange Markets to SPEEDEX

What remains is to discuss how to run the value computation in a manner that is fast and scalable. This section will get rather technical, and is not required for understanding the rest of this blog post. The following subsection in particular is not required for the rest of the discussion on price computation. This paper gives a more detailed discussion of the math behind the project.

Arrow-Debreu Exchange Markets

Internally, SPEEDEX views a batch of trades as an instance of an "Arrow-Debreu Exchange Market," a mathematical model initially developed by economists as a model for the global economy. In this model, there is a set of (divisible, fungible) assets, a set of autonomous agents, and an "auctioneer". Each agent possesses some units of some assets (their "endowment"), and has their own utility function that maps a set of amounts of some assets to some real number. The utility function quantifies the preference of an agent between two different sets of assets. (The version relevant here has none of the "firms," "production," or "stock dividends" in the original paper).

At some point, the auctioneer posts a set of asset prices. These prices are denominated in some fake unit of "money." Each user sells the entirety of their endowment to "the market," in exchange for this fake "money," and immediately buys back from the market (at the market prices) their preferred collection of assets (where "preference" is determined by the agent's utility function). Importantly, users have no utility for this fake "money," and spend all of it.

This should sound very similar to the SPEEDEX batch trading model, because it is. Trading one asset for another at a ratio of "valuations" is functionally identical to selling one asset for some fake "money," and then immediately spending that money on another asset. Users in SPEEDEX have linear utility functions. If one user wishes to sell asset A in exchange for B at a minimum price of 2 B per A, then that user implicitly values two units of B as at least as valuable as one unit of A. This user's utility function would thus be $$u(x)=x_A + x_B/2$$ Maximizing this utility function, subject to spending at most the number of units of fake money that the agent receives as payment for its endowment, means trading A for B if and only if the market exchange rate strictly exceeds the offer's minimum limit price.

Importantly, when agent utilities are linear, there exists a unique equilibrium of an Arrow-Debreu market, up to some technical conditions. An equilibrium in the Arrow-Debreu market is both a set of asset prices, and, for each agent, a set of assets bought from the market. This set of assets is almost always uniquely specified by the agent's utility function, but occasionally, the set of assets that maximizes an agent's utility function may not be unique. This occurs if an agent's limit price is equal to the market's offered exchange rate. In these cases, the equilibrium specifies which (among the options of equal utility) set of assets the agent receives.

The uniqueness means that the "virtual auctioneer" of SPEEDEX need only compute the equilibrium, and does not make any strategic choices of its own (e.g. between different equilibria).

Note that "uniqueness" means "uniqueness" up to technical conditions. Any equilibrium can always rescale its prices by a uniform quantity to construct a new equilibrium. Since this does not change the actual trade for any agent, we consider a rescaling of the prices to not actually constitute a distinct equilibrium. There also vacuously exist many equilibria if there is no trading activity between two sets of assets. In these cases, the auctioneer can choose any equilibrium without changing the real results for any trader. And sometimes, it might be an equilibrium for two traders to both trade or for neither to trade, if the trades go in opposite directions and have limit prices exactly equal to market prices. In these cases, the SPEEDEX auctioneer chooses the equilibrium that maximizes total trading activity.

Using the Arrow-Debreu model within SPEEDEX lets us leverage existing algorithms from the theoretical computer science literature as a starting point for our algorithms. With some modifications, we can make these algorithms run effectively in practice.

Tâtonnement

What we have found to be the most effective approach is one based on Tâtonnement, derived from the work of Codenotti, McCune, and Varadarajan. The algorithm itself is quite simple.

1. We start with a candidate set of prices. These might be uniformly one, for example, or they might be the prices SPEEDEX used to clear the previous batch of trades.
2. SPEEDEX computes how each trade responds to its candidate set, and adds up, for each asset, the total amount bought from the auctioneer (the demand) minus the amount sold to the auctioneer (the supply).
3. SPEEDEX adjusts its candidate prices. If demand for an asset exceeds its supply, SPEEDEX raises its price, and vice versa.
4. SPEEDEX repeats steps 2-3 until the demand for each asset equals its supply.
   

The price adjustment step is heuristically driven. The original paper of Codenotti et. al proposes to add to an asset's price the net demand (demand - supply) multiplied by a fixed constant step size. We find a substantial performance improvement by adjusting prices multiplicatively, and by weighting net demand by price. We also adjust the step size heuristically, and finally find that there are several other control parameters that wield much less influence on Tâtonnement's performance. Other works, such as that of Bei, Garg, and Hoefer, give alternative methods for adjusting prices in response to demand queries.

Note that this process works precisely because agents have linear utilities. When every agent has a linear utility, the net demand function (net demand, viewed as a function of the candidate set of prices) satisfies a property known as "weak gross substitutability." Intuitively, this property means that the market behaves in a predictable, Economics 101-style manner – if price goes up, demand goes down, and vice versa, and different asset prices do not interact in unexpected ways. (Formally, this property states that increasing the price of one asset should not cause a decrease in the demand for a different asset).

The expensive part of this algorithm is step (2). Naively done, this step would involve iterating over all offers during each loop iteration. While that work could be parallelized, it would still be a large amount of computational work that increases linearly as the number of open trade offers increases. On SPEEDEX, however, all trades are selling one asset in exchange for one other asset. SPEEDEX can thus group offers by the assets they trade and sort them by their limit prices. A trade offer with a low limit price will always execute at some candidate set of prices if a trade offer with a high limit price executes. As such, SPEEDEX can identify the set of offers that execute with only a binary search (one search per trading pair). One pre-computation pass over the whole set of trade offers thus enables subsequent queries to run in time that is only logarithmic in the number of open trade offers. This asymptotic acceleration is crucial for the scaling of SPEEDEX's price computation, and applies for any iterative, Tâtonnement-like algorithm.

Algorithms based on Tâtonnement also have the advantage of being simple to implement. Step 2 is a glorified for loop, and Step 3 is a small (carefully crafted) set of arithmetic equations – just a few dozen lines of code.

Accounting for Approximation Error with a Linear Program

While there exists a unique equilibrium for any instance of an Arrow-Debreu exchange market, the number of bits we would need to even write down the equilibrium can increase (possibly rather quickly) with the number of trades in the market. We also want an algorithm with a fixed runtime bound, and the theoretical runtime bounds ("polynomial") are not meaningful in practice.

As such, we will compute prices approximately. SPEEDEX runs Tâtonnement for a fixed number of iterations, or until prices meet a "close enough" criterion. We will then account for the error with a small linear program. This linear program asks, given a fixed set of prices, "what is the maximum amount of trading that the market can support at these prices?"

‍

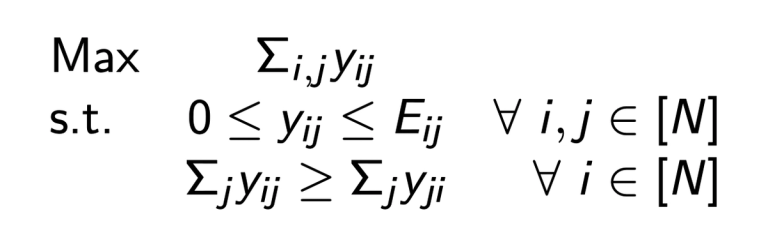
The variable \(y_{ij}\) denotes the price-weighted amount of asset \(i\) sold in exchange for asset \(j\), and the constant \(E_{ij}\) denotes the (price-weighted) maximum amount of asset \(i\) that is available for sale in exchange for \(j\).

This program has two nice features. First, its size has no dependence on the number of open trade offers, so the runtime of a solver does not depend on the size of the batch (and only depends on the number of assets traded on SPEEDEX). And secondly, the constraint matrix of the linear program is "totally unimodular." This means that the solution is integral, and the simplex algorithm (a standard algorithm for solving linear programs) can run without ever using non-integral values internally. As such, SPEEDEX need not use any floating-point arithmetic.

Even when prices are not exactly computed, every trader still gets the same exchange rates as every other trader in the batch. However, some traders that would wish to trade do not get to trade. We will say that the traders with low limit prices get priority over those with higher limit prices. In effect, a lower limit price means that a trader is less price sensitive and benefits more from trading than a trader with a limit price that is almost exactly the same as the market equilibrium price.

SPEEDEX and Buy Offers

Offers to buy a fixed quantity of one asset, in exchange for selling as little of another asset as possible (akin to PathPaymentStrictReceive) are computationally much more difficult to handle in conjunction with sell offers than just sell offers alone. They can be expressed within the Arrow-Debreu model as agents with piecewise linear utilities. However, integrating them directly into the price computation would move the computational problem into a complexity class known as PPAD, which is widely conjectured to admit no polynomial-time algorithms. By contrast, Arrow-Debreu instances with only linear utilities can be solved in polynomial time by some of the algorithms already discussed. One interesting open problem is to understand whether some buy offers could be directly integrated into the price computation without causing an empirical performance problem. Alternatively, buy offers could be integrated into the linear programming phase, without modifying the approximate price computation process.

----

To learn more about SPEEDEX, check out the following:

• My Meridian 2021 tech talk on the process of designing SPEEDEX.
• A standalone, open-source SPEEDEX implementation, implemented on its own blockchain (using HotStuff as a consensus protocol) is available here. We (myself and my coauthors, Professors Ashish Goel and David Mazières) give a detailed technical description of how this implementation works in this preprint.
• A prototype of an integration of SPEEDEX within Stellar-Core is available here.
• For a general overview on the conception and creation of SPEEDEX, check out this post on our main blog, or, for a more mathematical description and a discussion of some of the tradeoffs involved, see this workshop paper (by myself and Professors Goel and Mazières) or the preprint.