Detrás de Escena con SPEEDEX

Integrar SPEEDEX con Stellar requeriría tres cambios principales.

1. Un proceso de aplicación de libro mayor de varias fases

Stellar crearía un nuevo tipo de transacción "Conmutativa". Matemáticamente, dos operaciones "conmutan" si se pueden aplicar en cualquier orden sin cambiar el resultado final. Estas transacciones se ejecutarán como la primera fase de la aplicación de un libro mayor. Estas transacciones "conmutativas" solo podrían contener códigos de operación "conmutativos".

Inicialmente, el único código de operación "conmutativo" sería un nuevo código de operación "Crear Oferta SPEEDEX". SPEEDEX, por diseño, no depende del orden de las ofertas en un lote. Una operación, entonces, que simplemente agrega una nueva oferta de comercio a un conjunto no ordenado de ofertas naturalmente conmuta con cada otro código de operación "Crear Oferta SPEEDEX".

Estas transacciones generarían un lote de comercios para SPEEDEX. SPEEDEX luego calcularía precios y transferiría activos en consecuencia. Las ofertas que no se ejecuten inmediatamente en un lote no persistirán para el siguiente lote.

Finalmente, Stellar-core ejecutaría el resto de las transacciones en un libro mayor. Estas tendrían exactamente la misma semántica que las transacciones Stellar existentes.

En el futuro, Stellar podría agregar otros códigos de operación a la fase conmutativa. Paralelizar efectivamente la operación interna de Stellar-core requiere un trabajo de ingeniería significativo, por lo que la implementación inicial ejecutaría la fase conmutativa de manera serial. La operación interna podría entonces ser paralelizada sin realizar cambios en el protocolo. Y a largo plazo, es más efectivo y menos trabajo acelerar un protocolo que está diseñado para paralelizarse desde el principio, que acelerar un protocolo diseñado para ejecución serial (por ejemplo, con ejecución especulativa en una máquina virtual de contrato inteligente). Una regla general (la Regla de Conmutatividad Escalable de Clements et. al.) es que un conjunto de operaciones que conmutan puede ser paralelizado efectivamente.

2. Precondiciones Extendidas del Conjunto de Transacciones

SPEEDEX se basa en la garantía de que cada oferta de venta de un activo realmente puede proporcionar ese activo para la venta. Como el orden entre transacciones no debería importar, Stellar-core necesita verificar que no dos ofertas de comercio estén vendiendo las mismas unidades subyacentes de un activo (en otras palabras, Stellar-core necesita prevenir saldos negativos en las cuentas, lo que resultaría efectivamente en dobles gastos).

Stellar-core puede validar este requisito con una regla simple, asegurando que cada cuenta tenga suficientes activos para cubrir sus obligaciones de venta. Para un conjunto de transacciones dado, Stellar-core sumará todas las obligaciones de venta de cada cuenta. El conjunto de transacciones se consideraría inválido si las obligaciones de venta de cualquier cuenta exceden el saldo de la cuenta (para cualquier activo). Esta precondición esencialmente generaliza las verificaciones de saldo de XLM existentes del protocolo Stellar para pagar tarifas de transacción, y se puede implementar de manera análoga.

3. Activos Emitidos Limitados y Límites de Línea de Confianza

Los activos negociables en SPEEDEX estarían restringidos a tener, en total, solo INT64_MAX unidades emitidas en todo el ecosistema de Stellar. De nuevo, sin un orden de transacción, el protocolo de Stellar no tiene un método para resolver conflictos entre transacciones, y un conflicto que podría surgir en SPEEDEX es una cuenta recibiendo más de INT64_MAX unidades de un activo en total. Stellar puede evitar este problema limitando la cantidad total de cualquier activo emitido a lo máximo INT64_MAX unidades.

Este límite no necesitaría aplicarse a cada activo – solo aquellos negociados a través de SPEEDEX. El protocolo también requeriría que los usuarios establezcan sus límites de línea de confianza a INT64_MAX para transaccionar a través de SPEEDEX.

La versión más simple de SPEEDEX utiliza solo órdenes limitadas. Sin embargo, los algoritmos para el cálculo de precios, discutidos a continuación, y el modelo general de SPEEDEX también pueden mezclar naturalmente AMMs y órdenes limitadas con modificaciones mínimas. Y más importante, SPEEDEX podría aprovechar la funcionalidad AMM recientemente lanzada por Stellar sin ninguna modificación a los AMMs o a las transacciones "no conmutativas" regulares.

Un AMM puede responder a la pregunta "para mover la tasa de cambio marginal del AMM de su estado actual a la tasa de cambio del subastador, ¿cuánto de un activo tendría que vender el AMM al subastador?" El AMM recibiría entonces a cambio la cantidad correspondiente del otro activo del AMM, intercambiado a la tasa del subastador.

De los Mercados de Intercambio Arrow-Debreu a SPEEDEX

Lo que queda es discutir cómo ejecutar el cálculo de valor de una manera rápida y escalable. Esta sección se volverá bastante técnica, y no es necesaria para entender el resto de esta publicación de blog. La siguiente subsección en particular no es requerida para el resto de la discusión sobre el cálculo de precios. Este documento ofrece una discusión más detallada de la matemática detrás del proyecto.

Mercados de Intercambio Arrow-Debreu

Internamente, SPEEDEX ve un lote de comercios como una instancia de un "Mercado de Intercambio Arrow-Debreu," un modelo matemático inicialmente desarrollado por economistas como un modelo para la economía global. En este modelo, hay un conjunto de activos (divisibles, fungibles), un conjunto de agentes autónomos y un "subastador". Cada agente posee algunas unidades de algunos activos (su "dotación"), y tiene su propia función de utilidad que mapea un conjunto de cantidades de algunos activos a algún número real. La función de utilidad cuantifica la preferencia de un agente entre dos diferentes conjuntos de activos. (La versión relevante aquí no tiene ninguna de las "empresas", "producción", o "dividendos de acciones" en el papel original).

En algún momento, el subastador publica un conjunto de precios de activos. Estos precios están denominados en alguna unidad ficticia de "dinero". Cada usuario vende la totalidad de su dotación al "mercado", a cambio de este "dinero" ficticio, y de inmediato compra del mercado (a los precios de mercado) su colección preferida de activos (donde "preferencia" es determinada por la función de utilidad del agente). Importante, los usuarios no tienen utilidad por este "dinero" ficticio, y lo gastan todo.

Esto debería sonar muy similar al modelo de comercio por lotes de SPEEDEX, porque lo es. Comerciar un activo por otro a una relación de "valuaciones" es funcionalmente idéntico a vender un activo por algún "dinero" ficticio, y luego gastar inmediatamente ese dinero en otro activo. Los usuarios en SPEEDEX tienen funciones de utilidad lineales. Si un usuario desea vender el activo A a cambio del B a un precio mínimo de 2 B por A, entonces ese usuario implícitamente valora dos unidades de B al menos tan valiosas como una unidad de A. La función de utilidad de este usuario sería entonces $$u(x)=x_A + x_B/2$$ Maximizar esta función de utilidad, sujeto a gastar a lo más el número de unidades de dinero ficticio que el agente recibe como pago por su dotación, significa comerciar A por B si y solo si la tasa de cambio del mercado supera estrictamente el precio límite mínimo de la oferta.

Importante, cuando las utilidades de los agentes son lineales, existe un equilibrio único de un mercado Arrow-Debreu, sujeto a algunas condiciones técnicas. Un equilibrio en el mercado Arrow-Debreu es tanto un conjunto de precios de activos, y, para cada agente, un conjunto de activos comprados del mercado. Este conjunto de activos casi siempre es especificado de manera única por la función de utilidad del agente, pero ocasionalmente, el conjunto de activos que maximiza la función de utilidad de un agente puede no ser único. Esto ocurre si el precio límite de un agente es igual a la tasa de cambio ofrecida por el mercado. En estos casos, el equilibrio especifica cuál (entre las opciones de igual utilidad) conjunto de activos recibe el agente.

La unicidad significa que el "subastador virtual" de SPEEDEX solo necesita calcular el equilibrio, y no hace ninguna elección estratégica propia (por ejemplo, entre diferentes equilibrios).

Nota que "unicidad" significa "unicidad" sujeta a condiciones técnicas. Cualquier equilibrio siempre puede reescalar sus precios por una cantidad uniforme para construir un nuevo equilibrio. Ya que esto no cambia el comercio real para ningún agente, consideramos una reescalada de los precios como que no constituye un equilibrio distinto. También existen vacuamente muchos equilibrios si no hay actividad comercial entre dos conjuntos de activos. En estos casos, el subastador puede elegir cualquier equilibrio sin cambiar los resultados reales para ningún comerciante. Y a veces, podría ser un equilibrio que dos comerciantes comercien o que ninguno lo haga, si los comercios van en direcciones opuestas y tienen precios límite exactamente iguales a los precios de mercado. En estos casos, el subastador de SPEEDEX elige el equilibrio que maximiza la actividad comercial total.

Usar el modelo Arrow-Debreu dentro de SPEEDEX nos permite aprovechar algoritmos existentes de la literatura de ciencias de la computación teórica como un punto de partida para nuestros algoritmos. Con algunas modificaciones, podemos hacer que estos algoritmos funcionen efectivamente en la práctica.

Tâtonnement

Lo que hemos encontrado ser el enfoque más efectivo se basa en Tâtonnement, derivado del trabajo de Codenotti, McCune y Varadarajan. El algoritmo en sí es bastante simple.

1. Comenzamos con un conjunto de precios candidatos. Estos podrían ser uniformemente uno, por ejemplo, o podrían ser los precios que SPEEDEX usó para liquidar el lote anterior de comercios.
2. SPEEDEX calcula cómo responde cada comercio a su conjunto de candidatos, y suma, para cada activo, la cantidad total comprada del subastador (la demanda) menos la cantidad vendida al subastador (la oferta).
3. SPEEDEX ajusta sus precios candidatos. Si la demanda de un activo supera su oferta, SPEEDEX eleva su precio, y viceversa.
4. SPEEDEX repite los pasos 2-3 hasta que la demanda de cada activo iguala su oferta.
   

El paso de ajuste de precios es heurísticamente impulsado. El papel original de Codenotti et. al propone agregar al precio de un activo la demanda neta (demanda - oferta) multiplicada por un tamaño de paso constante fijo. Encontramos una mejora sustancial en el rendimiento ajustando los precios multiplicativamente, y ponderando la demanda neta por precio. También ajustamos el tamaño del paso heurísticamente, y finalmente encontramos que hay varios otros parámetros de control que ejercen mucho menos influencia en el rendimiento de Tâtonnement. Otros trabajos, como el de Bei, Garg y Hoefer, dan métodos alternativos para ajustar precios en respuesta a consultas de demanda.

Nota que este proceso funciona precisamente porque los agentes tienen utilidades lineales. Cuando cada agente tiene una utilidad lineal, la función de demanda neta (demanda neta, vista como una función del conjunto de precios candidatos) satisface una propiedad conocida como "sustitutabilidad bruta débil". Intuitivamente, esta propiedad significa que el mercado se comporta de una manera predecible, al estilo Economía 101 – si el precio sube, la demanda baja, y viceversa, y los precios de diferentes activos no interactúan de maneras inesperadas. (Formalmente, esta propiedad establece que aumentar el precio de un activo no debería causar una disminución en la demanda de un activo diferente).

La parte costosa de este algoritmo es el paso (2). Hecho de manera ingenua, este paso involucraría iterar sobre todas las ofertas durante cada iteración del bucle. Aunque ese trabajo podría ser paralelizado, todavía sería una gran cantidad de trabajo computacional que aumenta linealmente a medida que aumenta el número de ofertas de comercio abiertas. En SPEEDEX, sin embargo, todos los comercios están vendiendo un activo a cambio de otro activo. SPEEDEX puede así agrupar ofertas por los activos que comercian y ordenarlos por sus precios límite. Una oferta de comercio con un precio límite bajo siempre se ejecutará en algún conjunto de precios candidatos si se ejecuta una oferta de comercio con un precio límite alto. Como tal, SPEEDEX puede identificar el conjunto de ofertas que se ejecutan con solo una búsqueda binaria (una búsqueda por par de comercio). Un pase de precomputación sobre todo el conjunto de ofertas de comercio así permite que las consultas subsiguientes se ejecuten en un tiempo que es solo logarítmico en el número de ofertas de comercio abiertas. Esta aceleración asintótica es crucial para la escalabilidad del cálculo de precios de SPEEDEX, y se aplica para cualquier algoritmo iterativo, similar a Tâtonnement.

Los algoritmos basados en Tâtonnement también tienen la ventaja de ser simples de implementar. El paso 2 es un bucle for glorificado, y el paso 3 es un pequeño (cuidadosamente elaborado) conjunto de ecuaciones aritméticas – solo unas pocas docenas de líneas de código.

Contabilizando el Error de Aproximación con un Programa Lineal

Mientras existe un equilibrio único para cualquier instancia de un mercado de intercambio Arrow-Debreu, el número de bits que necesitaríamos incluso para escribir el equilibrio puede aumentar (posiblemente bastante rápido) con el número de comercios en el mercado. También queremos un algoritmo con un límite de tiempo de ejecución fijo, y los límites de tiempo de ejecución teóricos ("polinomiales") no son significativos en la práctica.

Como tal, calcularemos los precios aproximadamente. SPEEDEX ejecuta Tâtonnement por un número fijo de iteraciones, o hasta que los precios cumplan un criterio de "suficientemente cerca". Luego contabilizaremos el error con un pequeño programa lineal. Este programa lineal pregunta, dado un conjunto fijo de precios, "¿cuál es la cantidad máxima de comercio que el mercado puede soportar a estos precios?"

‍

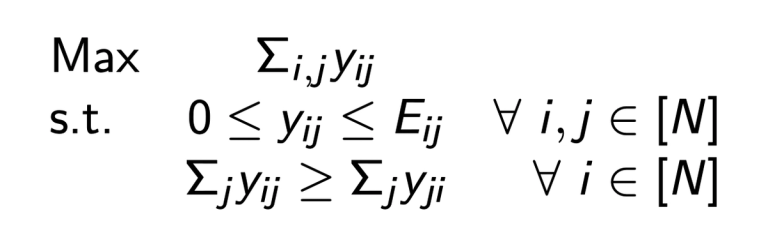
La variable \(y_{ij}\) denota la cantidad ponderada por precio del activo \(i\) vendido a cambio del activo \(j\), y la constante \(E_{ij}\) denota la cantidad máxima (ponderada por precio) del activo \(i\) que está disponible para la venta a cambio de \(j\).

Este programa tiene dos características agradables. Primero, su tamaño no depende del número de ofertas de comercio abiertas, por lo que el tiempo de ejecución de un solucionador no depende del tamaño del lote (y solo depende del número de activos comerciados en SPEEDEX). Y en segundo lugar, la matriz de restricciones del programa lineal es "totalmente unimodular." Esto significa que la solución es integral, y el algoritmo simplex (un algoritmo estándar para resolver programas lineales) puede funcionar sin usar nunca valores no integrales internamente. Como tal, SPEEDEX no necesita usar ninguna aritmética de punto flotante.

Incluso cuando los precios no se calculan exactamente, cada comerciante aún obtiene las mismas tasas de cambio que cualquier otro comerciante en el lote. Sin embargo, algunos comerciantes que desearían comerciar no llegan a hacerlo. Diremos que los comerciantes con precios límite bajos tienen prioridad sobre aquellos con precios límite más altos. En efecto, un precio límite más bajo significa que un comerciante es menos sensible al precio y se beneficia más del comercio que un comerciante con un precio límite que es casi exactamente el mismo que el precio de equilibrio del mercado.

SPEEDEX y Ofertas de Compra

Las ofertas para comprar una cantidad fija de un activo, a cambio de vender lo menos posible de otro activo (similar a PathPaymentStrictReceive) son computacionalmente mucho más difíciles de manejar en conjunto con ofertas de venta que solo ofertas de venta por sí solas. Se pueden expresar dentro del modelo Arrow-Debreu como agentes con utilidades lineales por tramos. Sin embargo, integrarlas directamente en el cálculo de precios movería el problema computacional a una clase de complejidad conocida como PPAD, que se conjetura ampliamente que no admite algoritmos en tiempo polinomial. Por contraste, las instancias de Arrow-Debreu con solo utilidades lineales pueden resolverse en tiempo polinomial por algunos de los algoritmos ya discutidos. Un problema abierto interesante es entender si algunas ofertas de compra podrían integrarse directamente en el cálculo de precios sin causar un problema de rendimiento empírico. Alternativamente, las ofertas de compra podrían integrarse en la fase de programación lineal, sin modificar el proceso de cálculo de precios aproximado.

----

Para saber más sobre SPEEDEX, consulta lo siguiente:

• Mi charla técnica en Meridian 2021 sobre el proceso de diseño de SPEEDEX.
• Una implementación independiente y open-source de SPEEDEX, implementada en su propia blockchain (usando HotStuff como protocolo de consenso) está disponible aquí. Nosotros (yo y mis coautores, los profesores Ashish Goel y David Mazières) damos una descripción técnica detallada de cómo funciona esta implementación en este preprint.
• Un prototipo de una integración de SPEEDEX dentro de Stellar-Core está disponible aquí.
• Para una visión general sobre la concepción y creación de SPEEDEX, consulta este post en nuestro blog principal, o, para una descripción más matemática y una discusión de algunos de los compromisos involucrados, vea este paper de taller (por mí y los profesores Goel y Mazières) o el preprint.