Verifying the Starbridge Protocol with Ivy

The Starbridge protocol is a protocol for bridging Stellar and Ethereum. In other words, it allows users to exchange native tokens on one chain for a wrapped version of those tokens on the other chain, and vice versa. Because Stellar does not support smart contracts yet, designing the Starbridge protocol poses unique challenges. Until Soroban is fully live on mainnet, we cannot rely on a smart contract to process withdrawal requests on Stellar. In this blog post, we explain how the Starbridge protocol makes use of existing features of the Stellar protocol to process withdrawal on Stellar, and how we used the Ivy verifier to validate that this part of the protocol is secure.

Before we start, note that, to keep things simple, we gloss over or even completely omit some important details. Our goal is not to offer a comprehensive Starbridge reference, but instead to explain some interesting aspects of the protocol.

To understand this blog post, you need to be familiar with the basic features of the Stellar protocol (such as token issuers, multi-sig accounts, sequence numbers, and transaction time bounds). If you need a refresher, head to the Stellar Docs (notably, Operations and Transactions and Issuing Assets). Moreover, for an introduction to the Starbridge project itself, see this earlier SDF blog post.

A Starbridge bridge consists of a smart contract on Ethereum, a set of bridge validators (which are independent servers on the Internet, meant to be operated by a diverse set of trustworthy organizations), and a multi-sig account on Stellar, the bridge account, that is controlled by the bridge validators.

Each Ethereum native token supported by the bridge, for example ETH, has a corresponding token on Stellar, for example wETH (where wETH stands for wrapped ETH), that is issued by the bridge account.

To transfer 1 ETH from Ethereum to Stellar, a user proceeds as depicted below. (1), the user deposits their 1 ETH in the bridge smart contract on Ethereum, which keeps the funds in custody. Then, (2) the user asks the bridge validators for a pre-signed Stellar transaction that mints 1 wETH on Stellar and transfers it to the user's account on Stellar. (3) The bridge validators check that the user's deposit is final on Ethereum, and if so, (4) return the requested, pre-signed transaction to the user. (5) Finally, the user then executes the transaction on Stellar, obtaining 1 wETH as a result.

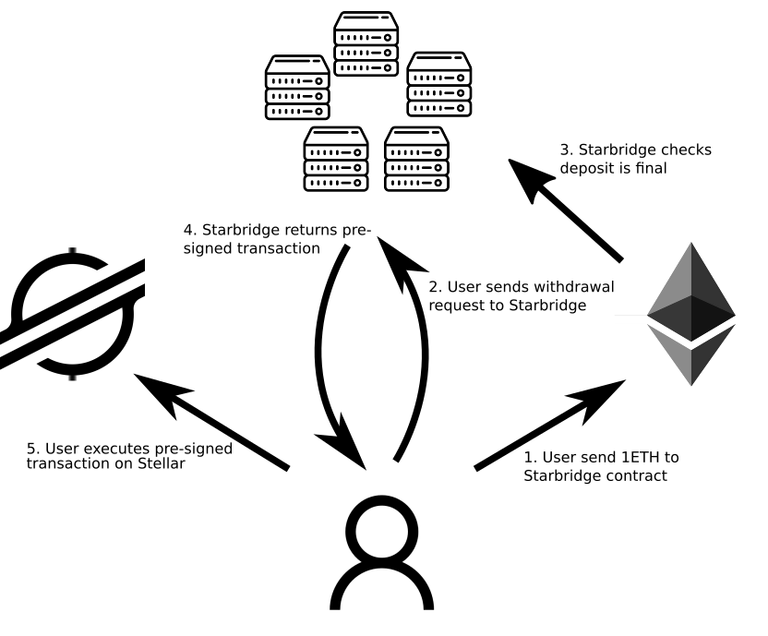
In the other direction, a user can exchange 1 wETH on Stellar for 1 ETH on Ethereum as follows. First, the user burns 1 wETH (e.g. by sending it to a forever-locked address). Then, the user asks the bridge validators to sign an attestation that the funds have indeed been burnt. Finally, the user calls the Starbridge smart contract on Ethereum, providing the attestation as proof that they can legitimately obtain 1 ETH. The Starbridge smart contract then deposits 1 ETH into the user's account on Ethereum.

Using pre-signed transactions poses one problem: a Stellar transaction can fail for a variety of reasons, for example when the sequence number of the transaction is not equal to the sequence number of the source account plus one, or when the receiving account does not have a trustline to the issuing account. So, a user might obtain a pre-signed transaction from the bridge validators but nevertheless be unable to withdraw their funds on Stellar because the pre-signed transaction fails. If that were to happen, the user's funds would remain stuck in the bridge contract on Ethereum.

We do not want users funds to be stuck in the bridge smart contract on Ethereum, and thus Starbridge allows users to request new, pre-signed withdrawal transactions from the bridge validators, even if they have already obtained one for the same deposit, or to request a refund of their ETH deposit on Ethereum.

Re-issuing withdrawal transactions and refunding deposits complicates things: Starbridge now has to make sure that an ETH deposit a) cannot be withdrawn as wETH twice and b) cannot be both withdrawn as wETH on Stellar and refunded on Ethereum. The Starbridge team devised a surprisingly simple way to support those features using the existing Stellar protocol. We now explain how it works at a high level.

Consider a user depositing 1 ETH in the Starbridge smart contract on Ethereum at time t0 (as given by the timestamp of the Ethereum block in which the user's deposit is executed). Bridge validators consider a withdrawal request valid between time t0 and t0+Δ, called the withdrawal period, where Δ is a configurable parameter that is agreed upon by all the bridge validators.

During the withdrawal period, the user can contact the bridge validators and request a pre-signed transaction depositing 1 wETH into their account on Stellar. Importantly, this pre-signed transaction must deposit the correct amount of wETH tokens in the user's account (here, 1 wETH), it must have a max-time t<t0+Δ, and it must have a sequence number equal to s+1, where s is the most recent sequence number of the user's account according to the Starbridge validators. (Note that, because of network delay, we cannot guarantee that the Starbridge validators will know about the most recent ledger externalized on Stellar; as we will see below, this does compromise the security of Starbridge.)

As we explained before, the pre-signed transaction returned by the Starbridge validators might fail once submitted to Stellar. This is not a problem, because the user can request a new pre-signed transaction as many times as they want. However, the same constraints as above apply to the transaction's max-time and sequence number.

For example, if the first pre-signed transaction has sequence number 2 (which would be okay if the user’s account has sequence number 1), but, by the time the user submits it to Stellar, their account’s sequence number increases to 2 and the transaction fails, the user can request a new pre-signed transaction with sequence number 3. Assuming that the Starbridge validators received the last externalized ledger (in which the user's account has sequence number 2), they will pre-sign the transaction with sequence number 3, which the user can submit to Stellar to obtain their 1 wETH. This example scenario is depicted below.

‍

After the withdrawal period has ended (i.e. when a Stellar ledger with close time tc>t0+Δ is externalized), all pre-signed transactions requested by the user become invalid because their max-time is equal to t0+Δ. At this point, Starbridge validators start granting refund requests to the user by returning, at the user's request, a signed message attesting that they agree to the refund. The user can then call the bridge smart contract on Ethereum, providing the signed refund requests as proof that the refund is legitimate. The smart-contract checks the signatures and, if they are valid, deposits 1 ETH back into the user's account. Crucially, the bridge validators only sign a refund request if the last externalized ledger they know of has a close time greater than the end of the withdrawal period and no corresponding withdrawal was executed by the user in any past ledger.

There are a few interesting things to note about this process:

• The Starbridge validators don’t need to synchronize between each other (they only need to agree on Δ): they process user requests independently of each other.
• The Starbridge validators must ingest Stellar ledgers and Ethereum blocks, but they might, temporarily, not know about the latest ledger closed by Stellar or the latest block produced by Ethereum. This might cause user requests and withdrawals to temporarily fail, but it will not compromise the safety of the bridge.
• The Starbridge validators can even crash and restart from a blank state (for example, because their hard drive failed and was replaced), and immediately start processing new withdrawal requests without having to worry about what they signed before crashing. In other words, the bridge validators are almost stateless, needing only to remember their keys; the rest can always be reconstructed from the chain state of Stellar and Ethereum.

Now, an important question is: how are we sure that there is not a clever way for a malicious user to subvert the protocol and withdraw their wETH twice? Or to both withdraw their wETH and get a refund on Ethereum? In other words, how are we sure that a clever user cannot steal from the bridge?

Intuitively, a) the clear separation between the withdrawal period and the refund period should prevent an ETH deposit to be both withdrawn on Stellar as wETH and also refunded on Ethereum, and b), double withdrawals should be prevented by the fact that the bridge validators only sign withdrawal transactions whose sequence number correspond to the last sequence number of the user's account that the bridge validators have heard of.

However, it is notoriously easy to miss a corner case and convince oneself that an incorrect distributed algorithm is correct. For example, the famous Chord algorithm (which implements a distributed hash table) was found to be incorrect more than 10 years after its publication; by that time, it had become one of the most cited works in computer science, but nobody noticed the mistake. There are many other examples like this.

Since a Starbridge deployment may have to secure millions of dollars in value, we would like to make sure that we did not overlook any corner case and that the protocol really makes it impossible to steal funds from the bridge. For this purpose, we created a formal model of the protocol and verified it using the Ivy verifier.

One important thing to note is that we did not verify the Starbridge implementation (i.e. the code written in Go and Solidity). Instead, we separately developed a model of the code, in the Ivy language, and verified that model. This allows us to verify that there are no design errors in the parts of the protocol that we modelled, but it does not preclude implementation errors.

In the rest of the blog post, we will briefly go over the model and the security proof, which are available in the docs/formal-model folder of the Starbridge repository.

We can think of the model as a program, written in the Ivy language, that simulates the transfer of tokens from Ethereum to Stellar. For simplicity, we model a single transfer from Ethereum to Stellar, and we assume that there is a single bridge validator.

To write a model in Ivy, we create variables representing the state of the different parties in the protocol, we specify their initial state, and we describe what are the possible actions that the parties can take. Each action consists of preconditions (keyword require) followed by a small piece of code that updates the state of the simulation in one atomic step.

For example, the variable bridge_ledger_time represents the closing time of the last ledger seen by the bridge validator, the variable executed(t, tx) is a boolean function indicating whether transaction t is executed in the ledger that closed at time t, and refunded is a boolean indicating whether the the bridge validator signed a refund request.

Given those state variables, the following action models the bridge validator signing a refund request:

1 action refund = {
2 require bridge_ledger_time > end_withdraw_period;
3 require forall T,TX . T <= bridge_ledger_time
4 -> ~executed(T, TX);
5 refunded := true;
6 }

Line 2 says that the closing time of the last ledger known to the bridge validator must be strictly greater than the end of the withdrawal period (in other words, the withdrawal period has ended). Line 3 says that no withdrawal transaction was executed by the time the withdrawal period ended (note that ~ means negation in Ivy). Finally, line 4, the refunded variable is updated to true to signify that the bridge validator signed the refund request.

We specify the other possible actions similarly. For example, below is the action corresponding to the bridge signing a withdrawal request (note that succ is the successor relation on sequence numbers). This action makes use of a new variable, pending(tx), which indicates whether the transaction tx has been signed by the bridge validator and is ready to be executed on Stellar.

1 action sign_withdraw(tx:withdraw_t) = {
2 require T <= bridge_ledger_time -> ~executed(T, TX);
3 require tx.max_time <= end_withdraw_period;
4 require tx.seqnum <= bridge_receiving_seqnu
| seqnum_t.succ(bridge_receiving_seqnum, tx.seqnum);
5 pending(tx) := true;
6 }

The other actions in the model are new_ledger, which models the Stellar network closing a new ledger, process_ledgers, which models the bridge validator learning about new closed Stellar ledgers, and restart, which models the bridge validator restarting from a blank state.

We can now express that the bridge is secure as using the following two correctness properties:

1 invariant forall T,TX . ~(refunded & exists T, TX. executed(T,TX))
2 invariant forall T1,TX1,T2,TX2 .
3 executed(T1, TX1) & executed(T2, TX2)
4 -> T1 = T2 & TX1 = TX2

Line 1, we state that it is not possible for the user's deposit to have been both refunded on Ethereum and withdrawn on Stellar. Line 2, we state that at most one withdrawal transaction can ever be executed. Together, those two properties imply that a user can never double-spend, regardless of how many withdrawal transactions they request and regardless of the timing of their actions.

Now that we have our model and the properties we want to check at hand, how do we actually verify that the properties hold? We could ask Ivy to enumerate the possible sequences of actions that can occur and check that the correctness properties are always satisfied. Unfortunately, there is an infinite number of combinations of actions (that's because, for example, sequence numbers are unbounded in the model, and the duration of the withdrawal period is arbitrary). We could consider only a fixed set of sequence numbers (e.g. 1, 2 and 3), and a withdrawal period of fixed length (e.g. 42), etc., in order to obtain a finite set of cases, and then check that no double spend occurs within those bounds by enumerating all possible sequence of actions. However, we wouldn't know if we missed a problem that occurs only with at least 4 sequence numbers, for example.

Instead, Ivy allows us to verify that no double spend can occur in any possible case, even if there are infinitely many. But for that, we need to help Ivy by providing an inductive invariant. An inductive invariant is a state predicate P such that a) P holds in the initial state, and b) if P holds and we execute an arbitrary action, then P holds again. Together, a) and b) imply that P will hold forever, regardless of which actions are taken and of their order.

Providing an inductive invariant makes Ivy's job much simpler: instead of having to consider arbitrary long and intricate sequences of actions, Ivy now just has to check properties a) and b), which only requires reasoning about a single protocol step at a time. In this case, Ivy is able to check this automatically for us.

The file starbridge.ivy contains a list of invariants that together form an inductive invariant and imply the correctness properties.

Want to dig deeper? The Ivy model and proof are available in the Starbridge repository, along with a Docker setup that makes it easy to run Ivy.

‍