Desmitificando el Proof-of-Agreement

Bob debe elegir un regalo de aniversario para su esposa Amy: flores o chocolate?

Bob confía en su amigo Cal y Cam, y en su suegra Deb. Podemos decir que tiene dos quórum para tomar una decisión sobre asuntos concernientes a Amy:

• Bob, Cal y Cam, y
• Bob y Deb.

Aquí hay un diagrama:

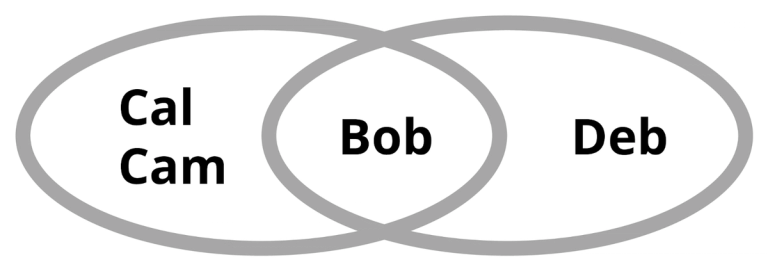
Para que Bob decida sobre un regalo de aniversario, se requiere el acuerdo dentro de al menos uno de estos quórum. Es decir:

• O bien Bob, Cal y Cam están de acuerdo,
• O Bob y Deb están de acuerdo.

También podría ser que Bob, Cal, Cam y Deb todos estén de acuerdo, pero esto no es necesario para decidir sobre un regalo.

Nota que hacer progreso es obligatorio; no es una opción para Bob rendirse y explicarle a Amy que no obtuvo su regalo de aniversario porque no pudo decidir qué obtener.

Así que para hacer progreso hacia la compra de un regalo adecuado, Bob necesita establecer las opiniones de Cal y Cam, y/o de Deb.

Pensemos como programadores y listemos todos los casos posibles:

1. Cal y Cam recomiendan flores. Deb recomienda flores también.
   
   Bob tiene que estar de acuerdo con al menos uno de sus quórum, y ya que ambos quórum están diciendo lo mismo, Bob no tiene opción: para progresar, debe estar de acuerdo con ellos y comprar flores.1
   
   
2. Cal y Cam recomiendan chocolate. Deb recomienda flores.
   
   Aquí, Bob tiene una elección: puede progresar con flores o chocolate. En cualquier caso, uno de sus quórum estará de acuerdo.
   Bob hace su elección lanzando una moneda, o podría usar conocimiento previo.
   
   
3. Cal recomienda chocolate, Cam recomienda flores. Deb recomienda flores.
   
   A menos que Bob pueda convencer a Cal o Cam de cambiar de opinión, Bob tiene que ir con flores.
   
   Esto es porque el quórum Cal, Cam, Bob no puede estar de acuerdo sin importar lo que Bob haga (porque Cal y Cam no están de acuerdo), pero Bob puede formar un quórum con Deb comprando flores.
   
   
4. Cal recomienda chocolate, Cam recomienda flores. Deb recomienda chocolate.
   
   Como en el caso 3, Bob no tiene opción: tiene que estar de acuerdo con Deb y comprar chocolate.

Comentarios sobre el ejemplo del aniversario

El ejemplo del aniversario captura algunos aspectos útiles de cómo funciona Stellar:

• La acción básica es transferencia de propiedad: de tokens en el caso de Stellar; de flores o chocolate en el caso de Bob arriba.
• Hacer progreso es obligatorio: Bob tiene que darle a Alice un regalo (asumiendo que quiere seguir casado), y Stellar tiene que hacer progreso (asumiendo que quiere retener a los usuarios).

También hay diferencias. El ejemplo del aniversario tiene un número fijo de (cuatro) participantes, dos quórum fijos, y solo una decisión. Stellar tiene docenas de nodos validadores, toma decisiones cada dos a cinco segundos – y, al menos en principio, nuevos nodos validadores pueden unirse en cualquier momento.

¿Cómo se gestiona este proceso?

Cuando un nuevo nodo validador se une a la red de Stellar, nomina un conjunto de rebanadas (también llamado un testigo). Un quórum es entonces cualquier conjunto de validadores tal que para cada validador en ese conjunto, una de sus rebanadas también está en ese conjunto.

Para ilustrar cómo funciona esto, volvamos a cuando Amy y Bob estaban planeando su boda. Estaban redactando su lista de invitados a la boda...

• Amy quería invitar a Bob (por supuesto), a su mejor amiga Che, y a su padre Dee.
  Así que Amy tiene una rebanada, que escribimos en notación de conjuntos matemáticos como sigue:
  ‍{Bob, Che, Dee}.
• Bob quería invitar a Amy (por supuesto), a sus padres Hal e Ivy, y al menos a uno de sus amigos Gia o Guy.
  Así que Bob tiene dos rebanadas:
  ‍{Amy, Hal, Ivy, Gia}
  y {Amy, Hal, Ivy, Guy}.
• A Che le va bien venir solo.
  Así que Che tiene una rebanada vacía:
  {}
  (o una rebanada, que es {Che}; es lo mismo).
• Dee solo vendrá si su esposa Deb puede venir también, y viceversa. Cada uno tiene una rebanada, que es el otro.
• Ivy solo vendrá si su hermana Kay viene también.
• Guy quiere traer a Jan o Joe. Así que Guy tiene dos rebanadas:
  {Jan}, y {Joe}.
• A Jan y Joe les va bien venir solos.

La lista de invitados tiene que ser un quórum: cada invitado debe tener al menos una de sus rebanadas en la boda.

Así que por ejemplo: Amy debe traer a Che y Dee, pero Bob puede traer (al menos) a uno de: Hal, Ivy, y Gia; o Hal, Ivy, y Guy. Realizando los cálculos vemos que las listas de invitados/quórum posibles (empezando desde Amy y Bob) son:

• {Amy, Che, Dee, Hal, Ivy, Gia, Deb, Kay}
• {Amy, Che, Dee, Hal, Ivy, Guy, Deb, Kay, Jan}
• {Amy, Che, Dee, Hal, Ivy, Guy, Deb, Kay, Joe}

Para tener una idea de cómo funciona esto, nota que:

• Una vez que agregamos a Amy, tenemos que agregar a Bob (ya está), Che, y Dee.
• Una vez que agregamos a Bob, tenemos que agregar a Amy (ya está) y Hal e Ivy – porque están en todas las rebanadas de Bob – pero podemos elegir si agregar a Gia o Guy.
• Una vez que agregamos a Guy, tenemos que agregar al menos a uno de Jan y Joe.
• Una vez que añadimos a Dee, nosotros tenemos que añadir a Deb, y viceversa (pero Dee ya está).

Continuando de esta manera, aumentamos la lista de invitados hasta alcanzar lo que los matemáticos llaman un punto fijo. Este es nuestro quórum.

Las listas de invitados anteriores son los quórums más pequeñosposibles. Quórums más grandes pueden hacer que la fiesta de boda sea más agradable, pero también más costosa. A menudo, las parejas resuelven el problema del quórum de la fiesta de boda invitando a todos, lo cual es una solución matemáticamente válida, aunque consume muchos recursos (para tomar otro término de programación).

Dejamos como ejercicio al lector crear un conjunto de rebanadas para el ejemplo del aniversario anterior. (¡La respuesta está en una nota al pie!2)

Stellar construye quórums a partir de rebanadas, justo como Amy y Bob hicieron cuando construyeron su lista de invitados.

• Empieza con algún participante o participantes (por ejemplo, Amy y Bob); luego
• para cada miembro del conjunto, añade una de sus rebanadas; y
• repite hasta que cada participante esté acompañado por (al menos) una de sus rebanadas.

En Stellar, las rebanadas representan confianza. Cuando te unes a la red como validador, tienes que decir qué rebanadas de los validadores existentes confías. Un quórum es un conjunto que puede progresar, en el sentido de que si está de acuerdo, entonces todos en el quórum están de acuerdo con al menos un grupo de confianza.

Repasemos la historia hasta ahora:

1. Cuando un validador se une a la red Stellar, nomina algunas rebanadas de confianza.
2. Un quórum es un conjunto de validadores que tiene al menos una rebanada de cada validador en el quórum.
3. Cuando un quórum está de acuerdo, puede progresar (por ejemplo, al comprometer una transacción en el libro mayor).

¿Qué impide que tal sistema se disuelva en el caos, con diferentes validadores en diferentes quórums comprometiendo diferentes transacciones? Para esto, necesitamos una definición técnica.

Definición 1.

1. Llama a dos participantes p y q entrelazados cuando cada quórum P de p intersecta con cada quórum Q de q.
2. Un topen es un quórum de participantes entrelazados.

En el Ejemplo 1 anterior, todos los participantes Cal, Cam, Bob y Deb están entrelazados, y el sistema consiste en un solo topen.

Volvamos a Amy y Bob. Viven en un bloque de pisos llamado Residencias Roma. Residencias Roma es uno de los tres bloques en el vecindario, los otros dos siendo Residencias Londres y Residencias París.

En la AGM (asamblea general anual) de Roma, las decisiones se toman por mayoría de votos. Así que los quórums son mayorías de participantes, y todos los residentes de Roma están entrelazados porque todos los conjuntos de mayoría se intersectan (de lo contrario no sería una mayoría). De manera similar para Londres y París. Sin embargo, los quórums de Roma no intersectan con los quórums de Londres o París, ni viceversa.

Así que este sistema se particiona en tres topens disjuntos, cada uno capaz de progresar independientemente: los consejos de AGM de Residencias Roma, Londres y París respectivamente. Esto es muy intuitivo: nosotros esperamos que estos comités actúen de manera autónoma y coherente dentro de sí mismos, y en terminología matemática simplemente decimos que estos son tres conjuntos de topen disjuntos.

Veamos dos ejemplos más concretos, para tener una idea de cómo funciona el estar entrelazado:

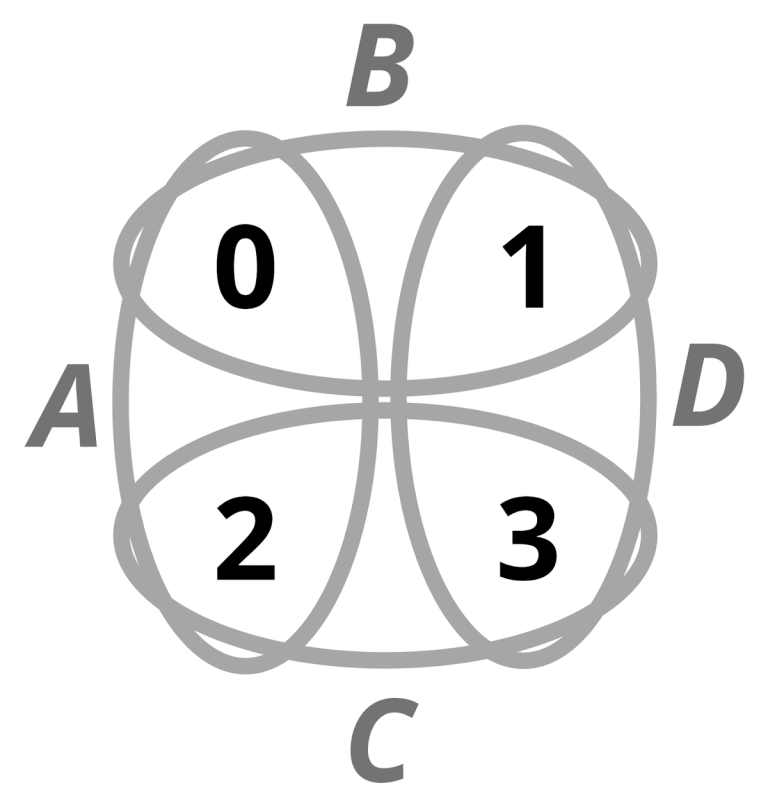
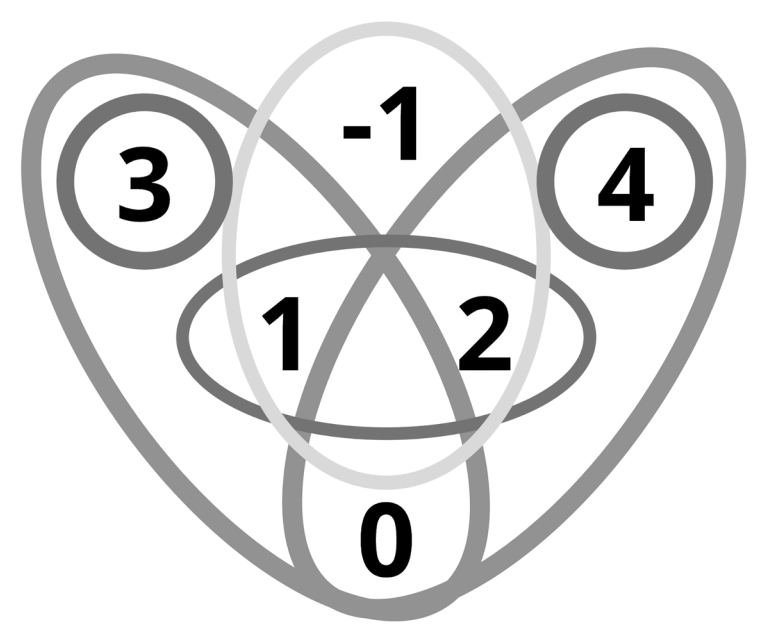
El ejemplo superior tiene cuatro quórums (etiquetados A, B, C y D) y todos los participantes están entrelazados.

En el ejemplo inferior el lector puede comprobar que 3 y 4 están entrelazados solo con ellos mismos, y -1, 1, 2 y 0 están entrelazados entre sí. Hay tres conjuntos de topen: 3; 4; y -1, 1, 2 (pero no -1, 1, 2, 0).3

El ejemplo de Roma/Londres/París anterior es canónico, porque se puede probar (usando matemáticas que no están en este post) que:

Lema 1.

Cualquier sistema de quórum se particionará en topens disjuntos (más quizás algunos puntos aislados).

El consenso está garantizado dentro de cada topen, por la propiedad de estar entrelazado: si cada participante está de acuerdo con su quórum, y todos los quórums en el topen se intersectan, entonces cada participante en el topen debe estar de acuerdo.

Se supone que los sistemas de blockchain son resilientes bajo ataque. Veamos cómo funciona esto en Stellar.

Supongamos que los residentes de París quieren corromper la toma de decisiones en Residencias Roma. Los residentes de París pueden añadir a los residentes de Roma a sus propias rebanadas (y así crear nuevos quórums) – pero no pueden cambiar las rebanadas de los residentes de Roma (cada participante decide sus propias rebanadas y solo sus propias rebanadas). Esto significa que el topen de los residentes de Roma – su consejo de AGM – no se ve afectado por el ataque, y Roma puede continuar tomando decisiones y progresando, completamente no afectado por el hecho de que están en las rebanadas de partes externas cuya confianza no reciproc

Este simple ejemplo importa particularmente porque es muy diferente de cómo funcionan blockchains como Ethereum, donde cualquiera en la red con computación o participación obtiene un asiento en la mesa de votación, no importa cuán desagradables puedan ser como persona u organización. En Stellar, solo obtienes un asiento en una mesa si puedes convencer a aquellos ya en esa mesa de que confíen en ti. O para poner esto en un lenguaje más técnico – la única manera de atacar la toma de decisiones de un topen es convencer a los miembros de ese topen de añadir al atacante a sus rebanadas. Un atacante no confiable no puede afectar su toma de decisiones, no importa cuán poderosos sean los computadores del atacante o cuán rico pueda ser el atacante.

En Stellar, la reputación – la confiabilidad – es todo. En algunos aspectos este es un sistema mejor que los sistemas basados en PoW o PoS (prueba de trabajo o prueba de participación): la confiabilidad es una construcción social, no una computacional, así que representar la confianza en el sistema da incentivos a los participantes para curar y mantener su reputación social – en otras palabras, para comportarse de una manera honesta y fiable. La reputación puede ser un predictor imperfecto de virtud, pero al menos, mientras cualquiera con recursos puede obtener hardware de minería o participación, no cualquiera puede ganar confianza y respeto.

En la vida real, hacer que Stellar funcione es un poco más complejo que los ejemplos anteriores. No podemos entrar en detalles aquí, pero nos gustaría dar al lector una idea de los problemas involucrados en aplicar estas ideas en la práctica.

El ejemplo relevante es bastante simple. Considera una elaboración del Ejemplo 1 anterior en el que todos los quórum tienen un tamaño de al menos tres:

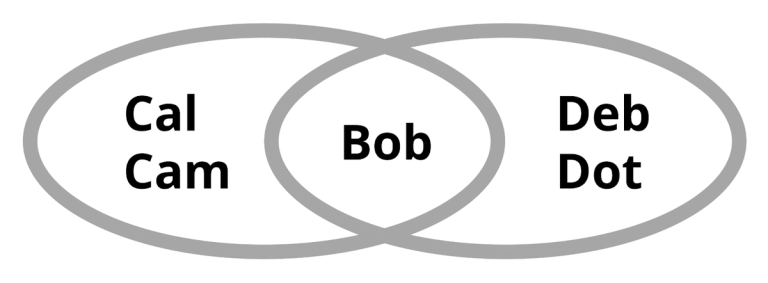
Todo lo que hemos hecho es agregar a Dot, la madre de Bob, al quórum que contenía a Deb, la suegra de Bob.

Este es un cambio simple, pero significa que si Cal y Cam no están de acuerdo, y también Deb y Dot no están de acuerdo, entonces el acuerdo del quórum es imposible independientemente de la votación de Bob (cualquier parecido con la vida real aquí es pura coincidencia, por supuesto).

En la vida real lo que sucede es que los quórums debaten entre sí hasta que uno de los quórums (con suerte) llega a un acuerdo y puede avanzar. (En la vida real esto siempre sucede de manera razonable, de buena fe y sin disputas ni rencor, por supuesto.) Algo similar se formaliza dentro del Stellar Consensus Protocol, por un mecanismo computacional que logra un consenso de manera confiable, en segundos. Esperamos con interés sumergirnos en este increíble logro técnico en otra publicación del blog.

---------------------

_{1. Podrías estar preguntándote qué pasa si Bob va y compra chocolates de todos modos. Bueno, podría hacerlo, pero eso simplemente no estaría jugando según las reglas. La vida está llena de tales situaciones, y el inglés tiene palabras positivas para aquellos que juegan según las reglas (reputable, reliable, trustworthy) y palabras negativas para los que no (disreputable, unreliable, untrustworthy).}

_{2. Una posibilidad es:}

• _{Bob tiene dos rebanadas: {Cal, Cam}, y {Deb}.}
• _{Deb tiene una rebanada, {Bob}.}
• _{Cal tiene una rebanada {Bob}.}
• _{Cam tiene una rebanada {Bob}.}

_{Otras rebanadas pueden generar los mismos quórums.}

_{3-1, 1, 2, y 0 no es un topen: todos los elementos están entrelazados, y contiene un quórum, pero no es en sí mismo un quórum.}[@portabletext/react] Unknown block type "span", specify a component for it in the `components.types` prop